머신러닝 - 선형회귀의 경사하강법 메모

학생 때 y = ax + b 라는 식을 자주 보곤 했다.

직선 그래프의 절편과 기울기로 x 값 y 값을 찾는 방식인데

 

선형회귀에도 비슷한 방식으로 사용된다 .

그러나 학생때는 x값 y값을 찾는것에 집중했다면 

딥러닝에서는 데이터를 예측하기 위해서 가장 적합한 기울기와 절편을 찾는데 집중한다.

 

기울기를 선형회귀에서는 가중치(W) 라고 부르고 b 를 bias 라고 부른다.

 

그럼 한번 코드를 보면서 이해해보자.

 

sklearn , 사이킷런이라고 부르는 파이썬으로 딥러닝을 공부할때 사용하기 유용한 데이터셋 라이브러리다.

 

여기서 내가 공부할때 참고한 당뇨병 환자 데이터를 가져와보겠다.

 

from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
print(diabetes.data.shape, diabetes.target.shape)

// 결과는 
(442, 10) (442,)

//이렇게 슬라이싱 하면
diabetes.data[0:3]
//결과는
array([[ 0.03807591,  0.05068012,  0.06169621,  0.02187235, -0.0442235 ,
        -0.03482076, -0.04340085, -0.00259226,  0.01990842, -0.01764613],
       [-0.00188202, -0.04464164, -0.05147406, -0.02632783, -0.00844872,
        -0.01916334,  0.07441156, -0.03949338, -0.06832974, -0.09220405],
       [ 0.08529891,  0.05068012,  0.04445121, -0.00567061, -0.04559945,
        -0.03419447, -0.03235593, -0.00259226,  0.00286377, -0.02593034]])

 

데이터를 가져오는건 아주 쉽다. 물론 준비된 데이터라서 그렇지 직접 어떤 모델을 만들고자 하면 데이터를 준비하는것 자체도 많은 노력이 들어간다.

 

미리 말을 하지 않았지만

이렇게 데이터를 직접 준비해서 트레이닝을 시키는것을 지도 학습이라고 부른다.

반대의 개념에는 비지도 학습이 있다.

 

이렇게만 보면 도대체 무슨 데이터인지 도통 알아볼수가 없다.그림으로 만들어보자.

 

import matplotlib.pyplot as plt

plt.scatter(diabetes.data[:, 2], diabetes.target)
plt.xlabel('x')
plt.ylabel('y')
plt.show()

plt 로 2차원 그림으로 만들어 낼 수 있다.

 

이런 그림이 나온다.

이제 진짜로 경사하강법에 대해 이야기를 해보자.

한번에 문장으로 표현하자면 

가장 데이터를 잘 표현할 수 있는 직선을 만들기 위해 가중치와 절편값을 반복하며 수정해나가고

최종적으로 가장 적합한 직선을 만들어내자!

 

일단 가장 먼저 생각 할 수 있는 최초의 직선을 그려보자.

 

w = 1.0 // 기울기
b = 1.0 // 절편

y_hat = x[0] * w + b // y_hat 의 결과값의 예측치 , x[0]은 데이터셋의 데이터
print(y_hat)
//print 결과  1.0616962065186886

print(y[0])
//print 결과 151.0

끔찍하다. 실제값과 예측값의 차이값이 150이나 난다. 엄청나다.

하지만 아직 아무런 수정도 하지 않았고 기울기나 절편을 1씩 줬으니 당연한 결과다.

 

이걸 최적의 값으로 찾아내는게 이번 글의 핵심이니까 따라해보자.

 

w_inc = w + 0.1
y_hat_inc = w_inc * x[0] + b
print(y_hat_inc)

가충치를 0.1 더해봤다.  결과는 

1.0678658271705574

아주 미세하게나마 정답에 가까워졌다 아주 미세하게.

우리는 이렇게 변화한 w의 변화률을 알아야한다. 그래야 계속해서 w를 바꿔 나갈 수 있다.

w_rate = (y_hat_inc - y_hat) / (w_inc - w)
print(w_rate)
w_new = w + w_rate
print(w_new)

변화률은 이렇게 구할 수 있다. 구하고는 새로운 w_new 에 더해서 w 의 값을 갱신해나가보자.

 

절편의 경우도 동일하다.

b_inc = b + 0.1
y_hat_inc = x[0] * w + b_inc
print(y_hat_inc)
//1.1616962065186887

b_rate = (y_hat_inc - y_hat) / (b_inc - b)
print(b_rate)
//1.0

b_new = b + 1
print(b_new)
//2.0

근데 이렇게 하나하나 더해주면서 찾아가면 답이 없다. 도대체 어느 세월에 다 할 수 있을까.

우리는 개발자니까 항상 더 효율적이고 좋은 방법을 찾아야한다.

 

그럼 이런 아이디어를 떠올려 볼 수 있다. 

실제값과 예측값의 차이값을 우리는 에러라고 생각할 수 있다. 그만큼 예측이 틀린것이니까.

이럼 이 에러의 크기에 비례해서 w와 b를 조정해나가면 더 빠르게 정답에 수렴하지 않을까?

에러값이 크면 그만큼 많이 수정이 필요하고 에러값이 작으면 그만큼 적게 수정하면 된다.

 

err = y[0] - y_hat
w_new = w + w_rate * err
b_new = b + 1 * err
print(w_new, b_new)
//10.250624555904514 150.9383037934813

전에 0.1 씩 더해주던것보다 훨씬 큰 폭으로 값이 변화했다.

 

여기서 알고 넘어가야할게 있다. err 는 "실제값 - 예측값" 인데 이건 양수가 될수도 음수가 될수도있다.

그런데 우리는 곱하기 연산을 하기 때문에 음수건 양수건 코드가 알아서 직선의 기울기를 조정한다.

멋진거 같다.

 

지금까지는 계속 y[0] , x[0]에 대해서만 진행했다.

모든 데이터를 다 해봐야하지 않겠는가?

 

for x_i, y_i in zip(x, y):
    y_hat = x_i * w + b
    err = y_i - y_hat
    w_rate = x_i
    w = w + w_rate * err
    b = b + 1 * err
print(w, b)

//587.8654539985689 99.40935564531424

파이썬의 zip 을 사용하면 x,y 에 있는 값들을 각각 하나씩 빼와서 for 문에 대입해서 돌리기 시작한다.

 

모든 x와 y에 대해서 연산하며 모든 값에 최적화된 가중치와 절편을 찾아간다.

 

그럼 한번 결과로 나온 w와 b로 다시 그림을 그려보자.

 

plt.scatter(x, y)
pt1 = (-0.1, -0.1 * w + b)
pt2 = (0.15, 0.15 * w + b)
plt.plot([pt1[0], pt2[0]], [pt1[1], pt2[1]])
plt.xlabel('x')
plt.ylabel('y')
plt.show()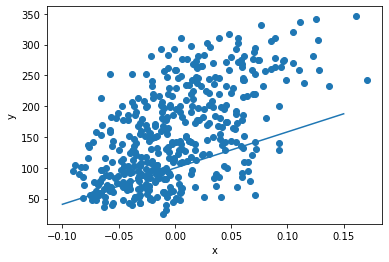

나쁘지 않다.

나쁘지는 않지만 아직 시원찮다. 어떻게 하면 더 맘에 들게 직선을 그릴 수 있을까?

많이 반복하면 된다. 여러번 반복하면 할때마다 조금씩 변화하면서 최적의 값을 찾아가게 될 것이다.

 

위의 포문을 100번 반복해보자.

 

for i in range(1, 100):
    for x_i, y_i in zip(x, y):
        y_hat = x_i * w + b
        err = y_i - y_hat
        w_rate = x_i
        w = w + w_rate * err
        b = b + 1 * err
print(w, b)

//913.5973364345905 123.39414383177204

다시 그림을 그려보면

 

훨씬 좋다

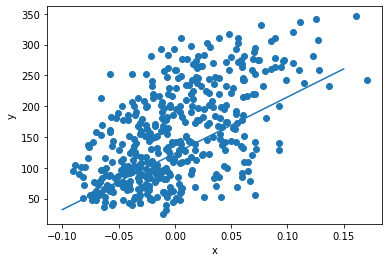
이제야 제대로 된 직선이 그려진다.

 

 

좋다!