문제설명
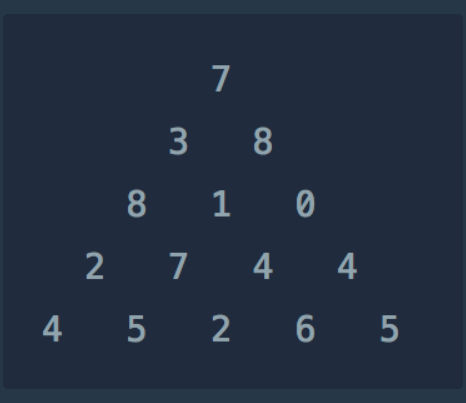
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.
삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.
제한사항
- 삼각형의 높이는 1 이상 500 이하입니다.
- 삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.
이 문제는 백준사이트에서도 풀어봤었다. (물론 그때는 오류가 나서 성공은 못했다.)
그래서 이번에는 맞춰버리겠다는 생각으로 풀어봤다.
dp 문제였는데 거쳐간 숫자의 최대값을 리턴하는 문제이므로 각 줄마다 내려오면서 합을 구하면서 내려와야하는 문제다.
나 같은 경우에는 삼각형이니까
1. 왼쪽 줄만 쭉 더하면서 내려왔을때.
2. 오른쪽 줄만 쭉 더하면서 내려왔을때.
3. 중간에 있는 숫자들에서는 현재 더하려는 값과 윗줄에서 왼쪽 대각선에 있는 값과 더했을때와 오른쪽 대각선에 있는값과 더한것 중 더 큰값을 삽입.
이런 틀을 가지고 시작했다.
일단 코드는 아래와 같다.
#include <string>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int dp[500][500];
int solution(vector<vector<int>> triangle) {
int answer = 0;
dp[0][0] = triangle[0][0];
//cout << dp[0];
for(int i=1;i<triangle.size();i++){ // 왼쪽만 다 더한거
dp[i][0] = triangle[i][0] + dp[i-1][0];
}
for(int i=1;i<triangle.size();i++){ // 오른쪽만 다 더한거
dp[i][i] = triangle[i][i] + dp[i-1][i-1];
}
for(int i=2;i<triangle.size();i++){ // 중앙
for(int j=1;j<triangle.size()-1;j++){
dp[i][j]= triangle[i][j] + max(dp[i-1][j-1],dp[i-1][j]);
}
}
for(int i=0;i<triangle.size();i++){
answer = max(answer , dp[triangle.size()-1][i]);
}
return answer;
}먼저 어떤 크기의 삼각형이던지 젤 위에 있는건
dp[0][0] = triangle[0][0]; 이 된다.
그리고 그 다음줄부터 연산을 시작하는데 첫번째 포문은
왼쪽에 있는 값들만 다 더한 부분
두번째 포문은 오른쪽만 다 더한것이다.
이렇게 하면 양쪽 끝의 값들은 계산이 되면서도 삼각형의 두번째 줄까지의 dp가 만들어진다.
그리고 세번째 포문을 시작하면
i=2 부터 시작하는데 이는 삼각형의 3번째 줄부터 연산을 하겠다는것을 의미한다.
이유는 두번째 줄까지는
7
3 8
이런 식이였기 때문에 딱히 대각선 왼쪽위, 대각선 오른쪽 위를 고려할 필요가 없었는데
3번째 줄부터는 이것을 고려해야한다.
그래서
dp[i][j]= triangle[i][j] + max(dp[i-1][j-1],dp[i-1][j]);
이런 코드가 필요하게 된다.
동작을 예를 들면
7
3 8
8 1 0
3번째 줄의 1을 거칠때 가장 큰 값이 되게 하려면 첫번째 줄과 두번째 줄에서 거쳐온 수의
합이 최대가 되어야 1을 거칠때도 임시적인 최대값이 될 수가 있다.
그럼 7과 3 을 거쳐서 온 경우와 7과 8 을 거쳐서 온 경우를 고려할 수 있는데
왼쪽 대각선 위와 오른쪽 대각선 위의 값의 max를 구하고 1과 더하면
1을 거칠때의 최대값을 알아올 수 있게 되는것이다.
이게 가능한 이유는?
위에서 말했듯 제일 왼쪽의 값의 합과 제일 오른쪽의 값의 합을 미리 구해놨기 때문이다.
그리고 마지막에 가장 아래줄의 dp 값들중 가장 큰 값을 출력하면
그것이 답이된다.
'알고리즘' 카테고리의 다른 글
| 프로그래머스 - 신고 결과 받기 (0) | 2022.03.21 |
|---|---|
| 1이 될때까지 최소 연산 횟수 (0) | 2021.08.21 |
| 알고스팟 - 소풍 (0) | 2020.06.15 |
| 알고스팟 - 보글게임(무식하게 풀기방법만 적용) (0) | 2020.06.15 |
| 프로그래머스 - 네트워크 (0) | 2020.04.19 |
| 프로그래머스 - 다리를 지나는 트럭 (0) | 2020.04.19 |
| 프로그래머스 - 가장 큰 수 (0) | 2020.04.13 |
| 프로그래머스 - 큰 수 만들기 (0) | 2020.04.12 |